大人気漫画『鬼滅の刃』には、数々の印象的な戦闘シーンがあります。
劇場版も公開されたので、18巻を読み返していたところ、衝撃のシーンが登場しました。上弦の参・猗窩座が見せた「素手で日輪刀を破壊する」というシーン。圧倒的な強さを示すものとして多くの読者に衝撃を与えた場面です。

しかし、ふと疑問に思いませんか?
「あれって実際にやるとしたらどれくらいの力が必要なんだろう?」
今回はそんな疑問を解決すべく、物理学の観点から猗窩座の規格外の一撃を、最新テクノロジーの塊である『生成AI Gemini 2.5Pro』の力を借りてマジメに計算してみました!
なお、私は高校ですら物理選択をしていないので何一つ分からないまま「そうなんだ」と回答を見ています。驚きの結果をぜひご覧ください。
問題のシーン:猗窩座が水柱の日輪刀を叩き割る!
このシーンが登場するのは、前述の通り単行本18巻の無限城での猗窩座と水柱・冨岡義勇の戦いです。激しい攻防の中、猗窩座は義勇の日輪刀を、なんと横から拳で叩きつけて破壊してしまいます。
鍛えに鍛えられた鋼であるはずの日輪刀を、いとも簡単に破壊する猗窩座。この描写は、上弦の鬼がいかに人知を超えた存在であるかを読者に強烈に印象付けました。
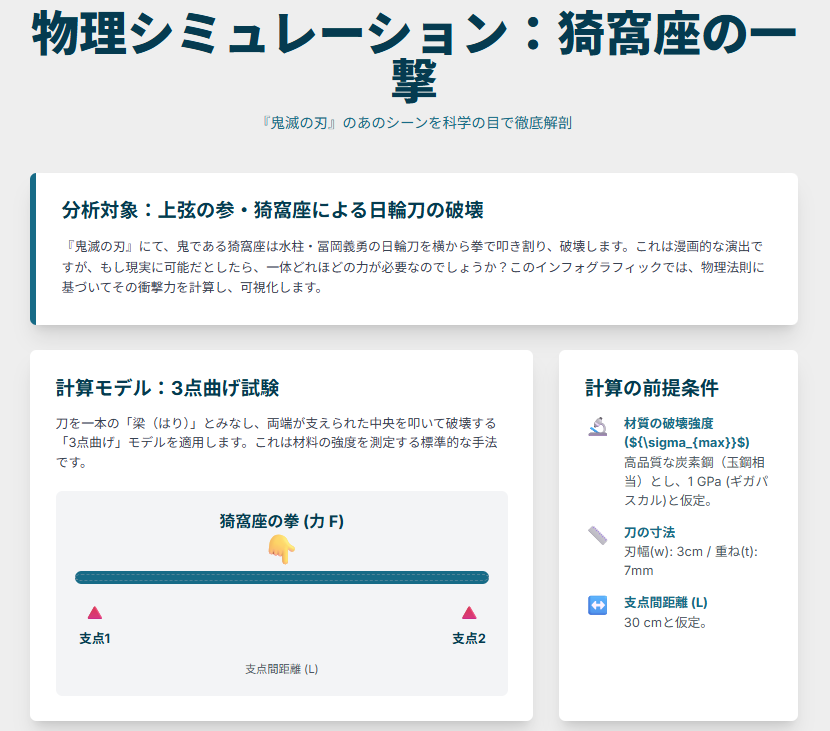
刀を折るための物理モデル「3点曲げ」とは?
さて、この現象を計算するために、今回は物理学や材料工学で使われる「3点曲げ試験」というモデルを応用します。
これは、対象物(今回は刀)を2点で支え、その間に力を加えて破壊強度を測るという、ごく一般的な手法です。身近な例で言えば、「膝の上に木の棒を置いて両手でへし折る」のをイメージすると分かりやすいかもしれません。
モノの強度について考えるときに一般的な測り方です。このシンプルなやり方で測れればそれに越したことはありません。まずはこのやり方で考えてみましょう。

疑問:「支点2」はどこ?
さて、さっそくですが皆さまはお気づきでしょう。
- 力点:猗窩座の拳
- 支点1:義勇が握る柄
- 支点2:???
「支点1は分かるけど、支点2はどこにあるの?」と。すでにだいぶ無理がありますが、考えられる可能性として、「慣性」を出してみましょう。
刀自身の「慣性」:猗窩座の一撃は音速に近いほどの超高速です。あまりに速く力が加わると、刀の先端部分は動きが追い付かず、その場に留まろうとします。この「その場に留まる力」が、瞬間的に見かけ上の支点として機能するのです。
ということにして、今回の計算では、これらの要素を理想化した「支点2」が存在すると仮定して進めます。
いざ計算!計算の前提と式
計算にあたり、以下の前提条件を設定しました。
- 刀の材質:日輪刀は特別な鋼ですが、ここでは高品質な工具用炭素鋼と同等とし、その破壊強度を1 GPa(ギガパスカル)とします。
- 刀の寸法:一般的な打刀を参考に、刃幅3cm、重ね(厚み)7mmとします。
- 支点間の距離:30cmと仮定します。
これらの前提を、材料強度を求める以下の公式に当てはめて、力(F)を算出します。
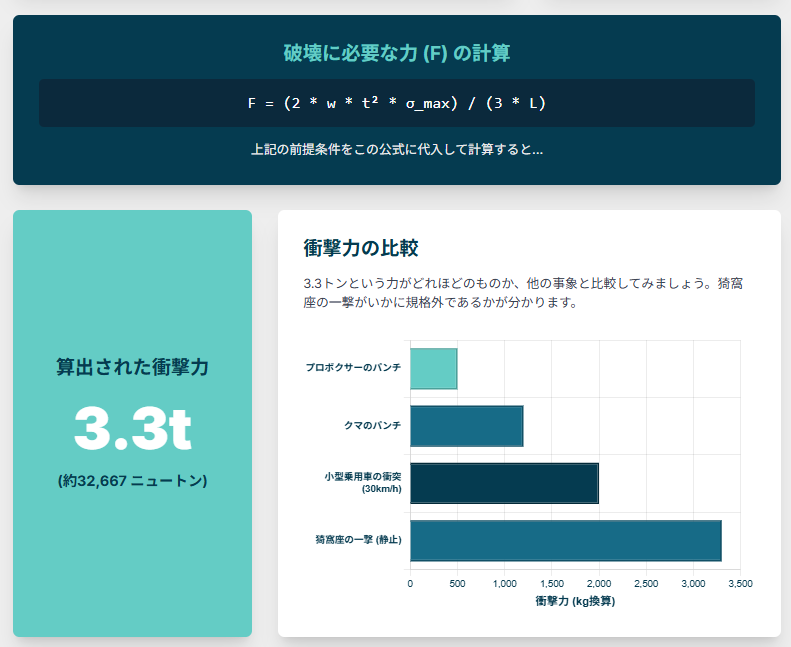
F = (2 × 刃幅 × 重ね² × 破壊強度) / (3 × 支点間距離)
計算結果:猗窩座の一撃の破壊力は…
緊張の計算結果です。猗窩座が日輪刀を破壊するために必要とした力は…
約3.3トン!!
という結果になりました!
物理的な単位であるニュートンに換算すると約32,667 Nとなります。これは、大型のSUVが全体重をかけてぶつかってくる衝撃に匹敵します。素手の一撃でこれほどの力を生み出すとは、まさに鬼の所業です。

人間では到達不可能な領域
この「3.3トン」という数値がどれだけ異常かというと、例えば世界トップクラスのプロボクサーのパンチ力が約500kgfと言われています。猗窩座はその6倍以上の力を簡単に出していることになります。
人間がどれだけ鍛錬を積んでも到達できない領域の力を、鬼たちは当たり前のように繰り出してくる。この絶望的なパワーの差こそが、『鬼滅の刃』の戦いの過酷さを物語っています。鬼になろう杏寿郎。
まだ続く:よく考えたら、義勇の刀は動いている
今回は「猗窩座の日輪刀破壊」を物理的に計算してみました。結果は以下の通りです。
- 物理モデルを適用すれば、計算上は破壊可能。
- ただし、必要な力は約3.3トンという超人的なもの。
- この分析によって、上弦の鬼の強さを改めて実感できる。
何気なく読んでいた漫画のワンシーンも、科学の目で見てみると新しい発見があって面白いですよね。今日はそんなことを検証してみました….
とここまで書いて気付いたのですが、よく考えたらこのシーンで重要なことって、義勇の刀が猗窩座に向かって振り下ろされたものだということですよね。止まっている刀を側面から叩いて折るのと、振り下ろした刀を折るのでは全然話が変わってくるはず。そもそも義勇の刀のスピードめちゃくちゃ速そうですし。
というわけで、もう1度計算してみます。
【再計算】動く刀をカウンターで破壊するということ
前回の計算は、あくまで「静止した刀」を折るためのものでした。しかし、このシーンの神髄は「振り下ろされる刀をカウンターで叩き折る」という、常軌を逸した神業にあります。

静止した物体を壊すのと、高速で動く物体を逆方向の力で破壊するのとでは、必要なエネルギーが桁違いに変わってきます。猗窩座の拳は、義勇の刀が持つ凄まじい運動エネルギーを完全に打ち消し(運動量ゼロにし)、さらに鋼を破壊するだけのエネルギーを与えなければなりません。
そこで、計算モデルをより現実に即した「動的衝突モデル」にアップデートし、再度計算に挑みます。
新たな前提条件:速度と衝突時間を加味する
今回の計算では、以下の新しい前提条件を追加します。
- 刀の速度:剣の達人である義勇の剣速は音速に迫るほどでしょう。ここでは衝突点での速度を控えめに見積もっても時速72km(秒速20m)と仮定します。
- 衝突時間:力が加わってから刀が破壊されるまでの時間は、極めて短い0.001秒と仮定します。
これらの条件を、運動量と力積の公式に当てはめていきます。
衝撃の再計算結果:猗窩座の一撃は、もはや災害レベル
さて、すべての条件を反映した再計算の結果が出ました。動く日輪刀をカウンターで破壊するために猗窩座が放った一撃の衝撃力は…
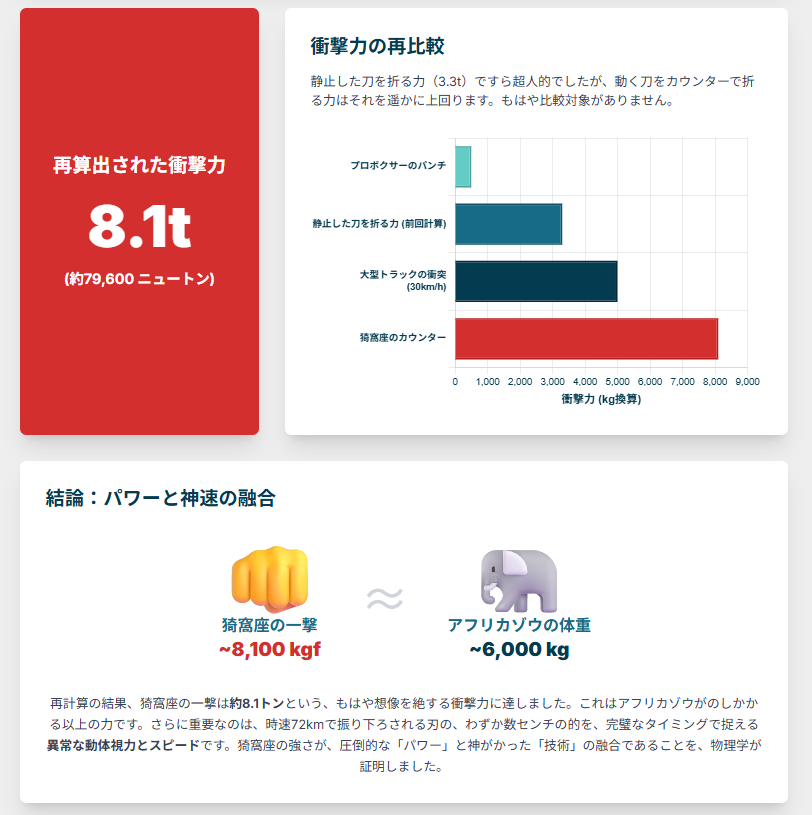
約8.1トン!!
前回の計算結果(3.3トン)を遥かに上回る、とてつもない数値が算出されました。これはもはや「パンチ」というより、一種の「爆発」に近いエネルギーです。
8.1トンという力がどれほどのものかというと、巨大なアフリカゾウ(約6トン)が全体重をかけてのしかかってくる以上の衝撃に相当します。これを人間サイズの拳の一点で生み出しているのですから、そのエネルギー密度は想像を絶します。

結論:猗窩座の強さは「パワー」と「技術」の融合
この再計算によって、私たちは猗窩座の本当の恐ろしさを垣間見ることができました。
重要なのは、単に8.1トンというパワーだけではありません。時速72kmで迫りくる刃の、わずか数センチの刀身を、完璧なタイミングで、正確に拳で捉える異常な動体視力、反射速度、そして精密な身体操作能力。このすべてが揃って初めて、この神業は成立します。
猗窩座の強さとは、圧倒的な「破壊力」と、それを完璧にコントロールする「武術の極致」とが融合した、まさに異次元のものでした。物理学の視点から見ても、彼が上弦の参という地位にいることに、一点の疑いもありません。
たった一つのシーンから、ここまでキャラクターの強さを読み解くことができるとは、改めて『鬼滅の刃』の奥深さを感じますね。
Geminiにここまで説明をしてもらいながら、私は物理学がまったく分からないのでファクトチェックもできないのですし、「そうなんだ・・・」って感じの感想になってしまいますが、こういうことを考えるのってなんだかおもしろいですよね。昔空想科学読本という本が好きだったのを思い出します。
お詳しい皆さま、ぜひぜひご意見お寄せ下さいませ。ありがとうございました。




![[バンダイ] 鬼滅の刃 DX日輪刀 ~ヒノカミ神楽~(対象年齢:6歳以上)](https://m.media-amazon.com/images/I/41t6lLMnqeL._SL160_.jpg)


コメント